


Next: Units and Values
Up: Mechanical Engineering Style Manual
Previous: Tables
Contents
Equations
The typesetting of mathematical equations is a complicated matter. The
Chicago Style Manual [1] has a whole chapter dedicated to it
and even that is lacking the finer points. The American Society of
Mathematics has published Mathematics into Type [14] by E.
Swanson. The scope of these books is far greater than that required by
a student to properly typeset simple equations.
One must understand that mathematical equations use a language with
nouns, verbs, etc. Swanson [14] gives this simple example:
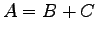 |
(2) |
In this case 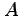 ,
, 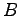 and
and 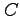 are nouns,
are nouns, 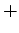 is a conjunction and
is a conjunction and 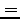 is a verb. Prove it to yourself by reading Equation 9.1
out loud.
is a verb. Prove it to yourself by reading Equation 9.1
out loud.
The other misunderstood fact about equations is that when
the letter P appears, one should read pressure. Hence equation
9.2 should be read as the pressure of the gas times the
volume of the gas is equal to the mass of gas times the gas constant
times the absolute temperature. It is not read as peevee equals
emartee which is meaningless. The guide to translating the symbols
into words is provided in the Nomenclature.
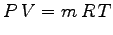 |
(3) |
Here are a few guidelines to correctly set your equations using a
modern equation typesetter such as Microsoft Equation
Editor
 , Math Type
, Math Type
 , TEX
, TEX
 or
LATEX
or
LATEX
 . Though these matematical typesetters are a
great help, their defaults cancause errors for the layman. For example,
the default for most of these software is a scalar variable, hence
everything is italicized. This is often incorrect.
. Though these matematical typesetters are a
great help, their defaults cancause errors for the layman. For example,
the default for most of these software is a scalar variable, hence
everything is italicized. This is often incorrect.
- Symbols that replace a number (variables or constants)
should be italicized. Hence it is
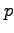 for pressure and not p. It
is
for pressure and not p. It
is 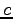 (velocity of light in vacuum, a constant) not c. This is also
true for indices and exponents. The specific heat of a gas at
constant pressure is
(velocity of light in vacuum, a constant) not c. This is also
true for indices and exponents. The specific heat of a gas at
constant pressure is 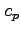 not
not
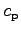 nor
nor
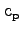 .
.
- Symbols that replace a word (often used in indices or in
chemistry) are set using the roman
![[*]](footnote.png) typeface. So the enthalpy of air
is
typeface. So the enthalpy of air
is
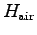 not
not 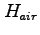 . All chemical symbols (H, He,
Li, Be, ...) and mathematical symbols (
. All chemical symbols (H, He,
Li, Be, ...) and mathematical symbols (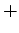 ,
, 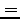 ,
, 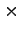 ,
...) follow this rule.
,
...) follow this rule.
- Use the roman font for functions like
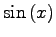 ,
,
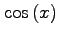 and
and 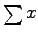 . You must differentiate between
the exponential function, e, and
. You must differentiate between
the exponential function, e, and 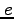 , the base of the natural
logarithms which has a value of 2.718281...The first is a
function, the second is a constant. This rule also applies to the
differential function. It is
, the base of the natural
logarithms which has a value of 2.718281...The first is a
function, the second is a constant. This rule also applies to the
differential function. It is
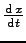 not
not
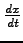 . Notice the thin space in the numerator to
differentiate that
. Notice the thin space in the numerator to
differentiate that
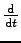 is an operator.
is an operator.
- Scalars are written in italics, vectors in bold italic
typeface and tensors in bold italic sans serif.
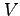 is velocity and
is velocity and 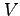 is speed.
is speed.
- When expressions include units, there is an unbreakable thin
space between the value and the units. Most equation typesetters
allow variable spacing.
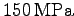 is appropriate whereas
150 MPa is not. Look closely, you can see a difference.
is appropriate whereas
150 MPa is not. Look closely, you can see a difference.
- The multiplication symbol,
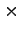 , should only be used
between numbers (not variables) or to indicate a vector product. Do not use it
between scalar variables as a space suffices to indicate the
product.
, should only be used
between numbers (not variables) or to indicate a vector product. Do not use it
between scalar variables as a space suffices to indicate the
product.
- Use scientific or engineering notation. Do not use computer
programming syntax to express numbers. The value of Avogadro's
number is
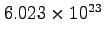 not 6.023E23 nor 6.023e23. This
usage was forced upon us because early computer output had but one
font and no way of indicating subscripts or superscripts. This is
still true in some programmes like Microsoft Excel
not 6.023E23 nor 6.023e23. This
usage was forced upon us because early computer output had but one
font and no way of indicating subscripts or superscripts. This is
still true in some programmes like Microsoft Excel
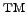 whose programmers think scientific notation requires a capital e.
Most of these problems can be avoided by a proper use of the SI.
whose programmers think scientific notation requires a capital e.
Most of these problems can be avoided by a proper use of the SI.
- Fractions are a common pitfall. Use the solidus, /, with
caution.
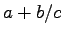 could mean
could mean
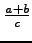 or
or
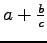 .
Parentheses help but can become unwieldy. Use Equation 9.3
instead of Equation 9.4:
.
Parentheses help but can become unwieldy. Use Equation 9.3
instead of Equation 9.4:
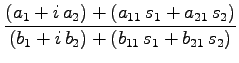 |
(4) |
![$\displaystyle \left[ \left(a_1+i a_2\right)+\left(a_{11} s_1+a_{21} s_2\righ...
...] / \left[ \left(b_1+i b_2\right)+\left(b_{11} s_1+b_{21} s_2\right) \right]$](img52.png) |
(5) |
- Try to avoid long subscripts and superscripts. Use
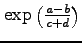 instead of
instead of
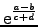 . When using variables with many
subscripts, the subscripts are separated by commas. The specific
heat of air at constant pressure is
. When using variables with many
subscripts, the subscripts are separated by commas. The specific
heat of air at constant pressure is
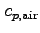 .
.
- Instead of repeating parentheses to mark groupings and
sub-groupings, alternate between parentheses, brackets and
braces
![[*]](footnote.png) preferably in this order:
preferably in this order:
Use Equation 9.5 as an example.
- Use the verb or conjunction to break long equations. In
Equation 9.5 the addition and subtraction
symbols (the conjunctions and less)
are used. In Equation 9.6 the break point is a verb (the equals
signs).
![\begin{displaymath}\begin{split}\left(\frac{\mathrm{d} \mathcal{B}} {\mathrm{d}...
...\rho \mathrm{d}V \right)_{t} } {\Delta t} \right] \end{split}\end{displaymath}](img57.png) |
(6) |
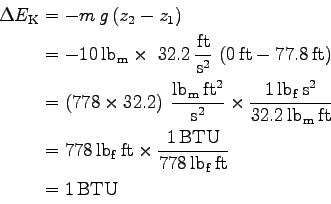 |
(7) |
- These rules are true for mathematical symbols no matter
where they appear in the text. Do not write a scalar variable
symbol in roman because it is in a paragraph. It should always
appear in italics.
Subsections



Next: Units and Values
Up: Mechanical Engineering Style Manual
Previous: Tables
Contents
Marc LaViolette
2006-01-13
![]() , Math Type
, Math Type
![]() , TEX
, TEX
![]() or
LATEX
or
LATEX
![]() . Though these matematical typesetters are a
great help, their defaults cancause errors for the layman. For example,
the default for most of these software is a scalar variable, hence
everything is italicized. This is often incorrect.
. Though these matematical typesetters are a
great help, their defaults cancause errors for the layman. For example,
the default for most of these software is a scalar variable, hence
everything is italicized. This is often incorrect.
![[*]](footnote.png) typeface. So the enthalpy of air
is
typeface. So the enthalpy of air
is
![[*]](footnote.png) preferably in this order:
preferably in this order: