


Next: Quotations, Paraphrases, Plagiarism and
Up: Equations
Previous: Units and Values
Contents
Choice of Nomenclature
The choice of which symbol represents which variable is often
difficult. The English alphabet having but 26 letters can be
augmented by the Greek one. See Table 9.2. The
Greek upper case letters are usually restricted to describe functions.
There are many upper case Greek letters that are the same as the Latin
ones (alpha, beta, epsilon, etc.). The commonly used mathematical
functions or operators are also given.
The International Organization for Standardization, ISO, has published
many standards giving the nomenclature to be used in certain fields of
study. It also has defined what SI should be. All of these standards
are available in Quantities and Units [2].
Table 9.2:
The Letters of the Greek Alphabet Used in the Typesetting
of Equations
| Name |
Lower case |
Upper case |
Function or Operator |
| Alpha |
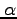
|
A |
|
| Beta |
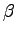
|
B |
Beta function |
| Gamma |
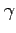
|
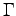
|
Gamma function |
| Delta |
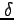
|
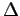
|
Increment |
| Epsilon |
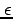 ,
,
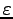
|
E |
|
| Zeta |
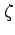
|
Z |
|
| Eta |
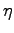
|
H |
|
| Theta |
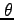 ,
, 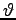
|
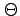
|
|
| Iota |
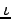
|
I |
|
| Kappa |
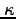
|
K |
|
| Lambda |
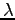
|
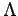
|
|
| Mu |
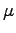
|
M |
|
| Nu |
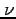
|
N |
Newman |
| Xi |
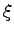
|

|
|
| Omicron |
o |
O |
|
| Pi |
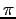 ,
, 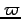
|
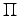
|
Multiplication |
| Rho |
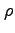 ,
, 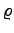
|
P |
Legendre polynomials |
| Sigma |
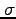 ,
, 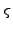
|
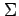
|
Summation |
| Tau |
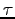
|
T |
|
| Upsilon |
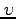
|
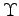
|
|
| Phi |
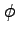 ,
, 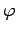
|
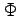
|
|
| Chi |
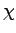
|
X |
|
| Psi |
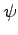
|
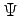
|
|
| Omega |
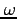
|
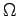
|
|
A part from those given in Table 9.2, many operators
have been attached to certain symbols. Those common in mechanical
engineering are given in Table 9.3. Also included in
that table are the preferred ways of writing certain functions. The
variable 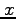 is used to clarify the notation.
is used to clarify the notation.
Table 9.3:
Common engineering operators or functions
| Operator/Function |
Symbol |
Notes |
| prime |
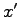
|
first derivative with respect to a length |
| double prime |
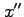
|
second derivative with respect to a length |
| dot |
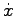
|
first derivative with respect to time |
| double dot |
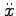
|
second derivative with respect to time |
| 10 base logarithm |
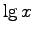
|
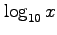 is sometimes used
is sometimes used |
| natural logarithm |
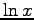
|
|
| inverse trigonometric |
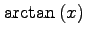
|
Do not use 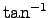 because of
confusion
because of
confusion |
| |
|
with the reciprocal
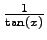
|



Next: Quotations, Paraphrases, Plagiarism and
Up: Equations
Previous: Units and Values
Contents
Marc LaViolette
2006-01-13